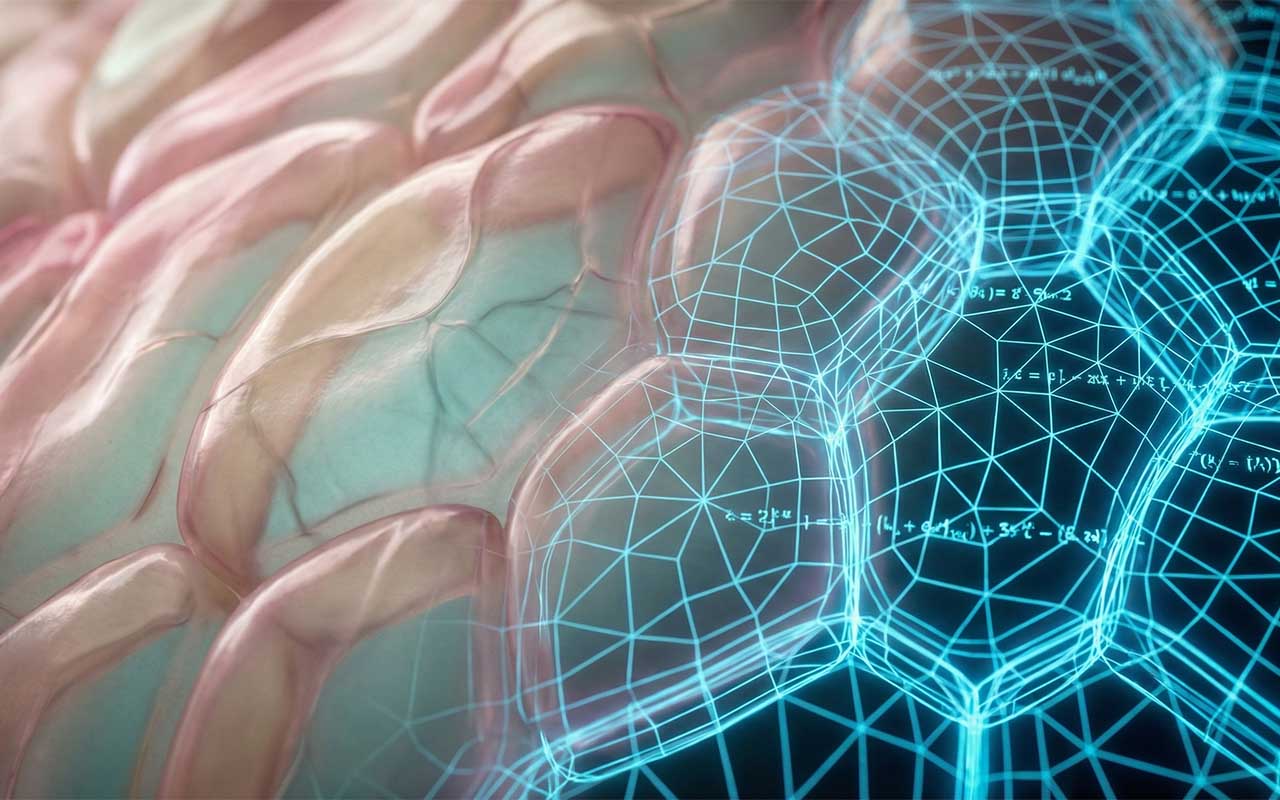
Kiedy myślimy o idealnym dopasowaniu elementów, wyobrażamy sobie łazienkowe kafelki – kwadraty, trójkąty lub sześciokąty. Geometria euklidesowa kocha ostre kąty i proste linie. Natura jednak ich nienawidzi. Jak więc to możliwe, że tkanki cebuli czy nasze własne mięśnie tworzą zwartą strukturę bez żadnych luk, mimo że składają się z obłych kształtów? Odpowiedź na to pytanie właśnie znaleźli matematycy, a ich odkrycie rewolucjonizuje nasze postrzeganie świata ożywionego.
Przez stulecia naukowcy i artyści głowili się nad zagadką naturalnych wzorów. Jeśli śledzicie najnowsze doniesienia ze świata nauki, wiecie, że natura rzadko działa chaotycznie. Wszystko, od plastra miodu po łuski ryb, ma swój matematyczny porządek. Jednak klasyczna teoria tesselacji (wypełniania płaszczyzny) miała poważną lukę: nie potrafiła wyjaśnić, jak szczelnie wypełnić przestrzeń elementami o zakrzywionych krawędziach. Aż do teraz. Międzynarodowy zespół badaczy zidentyfikował i opisał nową klasę kształtów geometrycznych, które nazwali „miękkimi komórkami” (ang. soft cells).
Dlaczego natura unika ostrych narożników?
Tradycyjna matematyka mówi nam, że aby wypełnić płaszczyznę bez pozostawiania pustych przestrzeni, potrzebujemy wielokątów. Jednak w biologii ostre narożniki są problematyczne – są punktami słabymi strukturalnie i trudnymi w utrzymaniu dla żywych organizmów. Komórki biologiczne dążą do zaokrągleń, aby minimalizować napięcie powierzchniowe.
Problem polegał na tym, że koła czy elipsy nie pasują do siebie idealnie – zawsze zostawiają wolne przestrzenie (widać to, gdy próbujemy ułożyć obok siebie monety). Nowo odkryte „miękkie komórki” rozwiązują ten dylemat. Są to kształty o zakrzywionych krawędziach, które posiadają minimalną liczbę ostrych wierzchołków (zwykle tylko dwa), a mimo to potrafią zazębiać się ze sobą, tworząc jednolitą, szczelną powierzchnię. To geometryczny odpowiednik puzzli, które natura układała od milionów lat, a które my dostrzegliśmy dopiero dzisiaj.
Od muszli łodzika do przekroju cebuli
Odkrycie to nie jest jedynie abstrakcyjną zabawą matematyków. Badacze, w tym prof. Gábor Domokos z Budapesztu (znany z odkrycia gömböca), wykazali, że „miękkie komórki” występują w przyrodzie powszechnie. Idealnym przykładem w 2D są komórki widoczne w przekroju cebuli czy struktura skrzydeł owadów. W trójwymiarze zasada ta tłumaczy budowę tkanki mięśniowej.
Kluczem do zrozumienia tego fenomenu jest ewolucja geometryczna. Kształty te ewoluują od form ostrych do zaokrąglonych, zachowując zdolność do szczelnego wypełniania przestrzeni. To właśnie ta elastyczność pozwala organizmom rosnąć i zmieniać kształt bez naruszania integralności tkanki. „Miękkość” tych geometrycznych form jest więc warunkiem koniecznym dla istnienia złożonego życia.
Architektura przyszłości inspirowana biologią
Zidentyfikowanie reguł rządzących „miękkimi komórkami” otwiera drzwi nie tylko do lepszego zrozumienia anatomii, ale także do nowych rozwiązań w inżynierii i architekturze. Skoro natura wykorzystuje te kształty do tworzenia wytrzymałych i elastycznych struktur, inżynierowie mogą zacząć projektować materiały naśladujące te właściwości – np. powłoki, które są jednocześnie szczelne i odporne na naprężenia w sposób, jakiego nie oferują tradycyjne siatki geometryczne.
To fascynujące, że po tysiącach lat studiowania geometrii, wciąż uczymy się podstaw od najstarszego architekta świata – ewolucji. To, co dla nas jest nowym wzorem matematycznym, dla natury jest standardem budowlanym stosowanym od zarania dziejów.